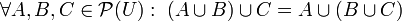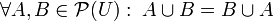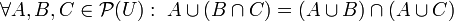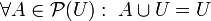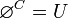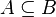Introducción
Álgebra de Boole en informática y matemática, es una estructura algebraica que esquematiza las operaciones lógicas And, Nand, Or, Nor, Not. Así como el conjunto de operaciones unión, intersección y complemento.
En Lógica binaria se suele emplear la notación

, común en la tecnología digital, siendo la forma más usual y la más cómoda de representar.
Por ejemplo las leyes de De Morgan se representan así:


Cuando el álgebra de Boole se emplea en electrónica, suele emplearse la misma denominación que para las
puerta lógica AND (Y), OR (O) y NOT (NO), ampliándose en ocasiones con X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia). las variables pueden representarse con letras mayúsculas o minúsculas, y pueden tomar los valores {0, 1}
Empleando esta notación las leyes de De Morgan se representan:
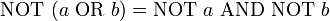

En su aplicación a la
lógica se emplea la notación
y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
Con la notación lógica las leyes de De Morgan serían así:
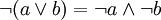

En el formato de Teoría de conjuntos el Álgebra de Boole toma el aspecto:
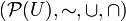
En esta notación las leyes de De Morgan serían así:
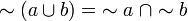
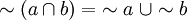
Otra forma en la álgebra de conjuntos del Álgebra de Boole, las leyes de De Morgan serían así:


Desde el punto de vista práctico existe una forma simplificada de representar expresiones booleanas. Se emplean apóstrofos (') para indicar la negación, la operación suma (+) se representa de la forma normal en álgebra, y para el producto no se emplea ningún signo, las variables se representan, normalmente con una letra mayúscula, la sucesión de dos variables indica el producto entre ellas, no una variable nombrada con dos letras.
La representación de las leyes de De Morgan con este sistema quedaría así, con letra minúsculas para las variables:
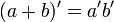

y así, empleando letras mayúsculas para representar las variables:

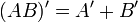
Todas estas formas de representación son correctas, se utilizan de hecho, y pueden verse al consultar bibliografía. La utilización de una u otra notación no modifica el álgebra de Boole, solo su aspecto, y depende de la rama de las matemáticas o la tecnología en la que se esté utilizando para emplear una u otra notación.
Hay numerosos casos de distintos análisis de estructuras algebraicas que corresponden al álgebra de Boole, aunque en apariencia son muy diferentes, su estructura es la misma. Vamos a ver algunos de ellos, con el propósito de hacer palpable las similitudes en la estructura y los distintos ámbitos de aplicación y distinta terminología para referirse a las operaciones o a las variables.
Una serie de temas, aparentemente tan distintos, tiene dos cosas en común, la lógica binaria basada en los ceros y los unos y el álgebra de Boole, posiblemente la forma más conocida de esta álgebra, que en ocasiones da lugar a la interpretación que el álgebra de Boole es la lógica binaria exclusivamente, así el conjunto
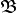
en este caso está formado por dos elementos {0,1}, o {F, V}, o {no, sí}, dos valores contrapuestos, que son las dos posibles alternativas entre dos situaciones posibles, aquí, sin perdida de la generalidad, tomaremos el conjunto: {0,1} como ya hemos dicho:

Donde:


- La operación unaria interna, que llamaremos negación:
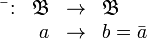
La operación unaria interna negación, definimos una aplicación que a cada elemento a de {0,1}, le asigna un b de {0,1}.

Para todo elemento a en {0.1}, se cumple que existe un único b en {0,1}, tal que b es la negación de a. Como se ve en la tabla.
- La operación binaria interna, que llamaremos suma:

Con la operación suma definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.

Para todo par ordenado (a,b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de sumar a con b.
- la operación binaria interna, que llamaremos producto:

Con la operación producto definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.
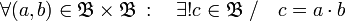
Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado del producto a y b. Como se puede ver en la tabla.
Axiomas
Así

es un
álgebra de Boole al cumplir los siguientes axiomas:
- 1a: La ley asociativa de la suma:
-

- 1b: La ley asociativa del producto:
-

- 2a: Existencia del elemento neutro para la suma:
-
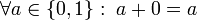
- 2b: Existencia del elemento neutro para el producto:
-

- 3a: La ley conmutativa de la suma:
-

- 3b: La ley conmutativa del producto:
-

- 4a: Ley distributiva de la suma respecto al producto:
-
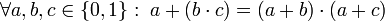
- 4b: Ley distributiva del producto respecto a la suma:
-

- 5a: Existe elemento complementario para la suma:
-

- 5b: Existe elemento complementario para el producto:
-
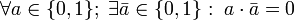
Luego

es álgebra de Boole.
Teoremas fundamentales
Partiendo de estos axiomas se puede demostrar los siguientes teoremas:
- 6a: Ley de idempotencia para la suma:
-

- 6b: Ley de idempotencia para el producto:
-

- 7a: Ley de absorción para la suma:
-

- 7b: Ley de absorción para el producto:
-

- 8a: Ley de identidad para la suma:
-
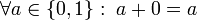
- 8b: Ley de identidad para el producto:
-

-

-

-

-

-

Orden en el álgebra de Boole
Partiendo de

álgebra de Boole, dadas dos variables binarias:
a,
b, que cumplen alguna de estas condiciones:

entonces a es menor o igual que b. Dados los valores binarios 0 y 1, podemos ver:




Estas cuatro condiciones son equivalentes y el cumplimiento de una de ellas supone el cumplimiento de las otras, en este caso es sencillo comprobarlas todas. Luego podemos decir que 0 antecede a 1 y lo denotamos:

Si además sabemos que 0 y 1 son valores distintos:

El valor binario 0 es menor que el valor binario 1.
Partiendo de un conjunto
U, cualesquiera, llamamos
conjunto potencia de
U, al conjunto de todos los subconjuntos posibles de
U y lo denotamos

.
A título de ejemplo podemos considerar:

Que tiene como conjunto potencia:

Donde podemos definir:

Y como es obvio:


- La operación unaria interna, que llamaremos complemento:

En esta operación definimos una aplicación que, a cada elemento A de P(U), le asigna un B de P(U).

Para todo elemento A en P(U), se cumple que existe un único B en P(U), tal que B es el complemento A.
Definiendo el complemento de un conjunto así:

B es el complemento de A, si se cumple que para todo x que pertenezca a B, x pertenece a U y x no pertenece a A.
- La primera operación binaria la llamaremos unión:

Con esta operación binaria interna definimos una aplicación que, a cada par ordenado (A, B) de P(U) por P(U), le asigna un C deP(U).

Para todo par ordenado (A,B) en P(U) por P(U), se cumple que existe un único C en P(U), tal que C es la unión A y B.
Definiendo la unión de dos conjuntos como:

El conjunto C es la unión de A y B, si para todo elemento x de C, se cumple que x es elemento de A o de B
- La segunda operación binaria la llamaremos intersección:

Con lo que definimos una aplicación que, a cada par ordenado (A, B) de P(U) por P(U), le asigna un C de P(U).

Para todo par ordenado (A,B) en P(U) por P(U), se cumple que existe un único C en P(U), tal que C es la intersección A y B.
Definiendo la intersección de dos conjuntos como:

El conjunto C es la intersección de A y B, si para todo elemento x de C, se cumple que x es elemento de A y de B.
Axiomas
Con lo que podemos plantear:

, para un
U conocido, como
álgebra de Boole si cumple las siguientes axiomas:
- 1a: La ley asociativa de la unión:
-
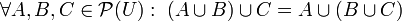
- 1b: La ley asociativa de la intersección:
-

- 2a: Existencia del elemento neutro para la unión:
-

- 2b: Existencia del elemento neutro para la intersección:
-

- 3a: La ley conmutativa de la unión:
-
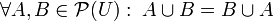
- 3b: La ley conmutativa de la intersección:
-

- 4a: Ley distributiva de la unión respecto de la intersección:
-
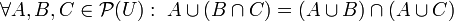
- 4b: Ley distributiva de la intersección respecto a la unión:
-

- 5a: Existe elemento complementario para la unión:
-

- 5b: Existe elemento complementario para la intersección:
-

Concluyendo que

es un álgebra de boole.
Teoremas fundamentales
Partiendo de estos axiomas se puede demostrar los siguientes teoremas:
- 6a: Ley de idempotencia para la unión:
-

- 6b: Ley de idempotencia para la intersección:
-

- 7a: Ley de absorción para la unión:
-
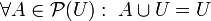
- 7b: Ley de absorción para la intersección:
-

- 8a: Ley de identidad para la unión:
-

- 8b: Ley de identidad para la intersección:
-

-

-

-
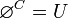
-

-

Orden en el álgebra de Boole
Dado

álgebra de Boole, podemos comprobar:




Para los conjuntos A y B que cumplen estas propiedades, podemos decir que A antecede a B, que en el caso de conjuntos se diría A es igual o un subconjunto deB y lo denotamos:
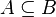
Entendiéndose que A es igual o un subconjunto de B cuando:

El conjunto A es igual o un subconjunto de B, si para todo elemento x que pertenezca a A, x pertenece a B.
También se puede comprobar:

Para todo A de las partes de U, si se cumple que: la unión de A y U es U, la intersección de A y U es A, la unión del complemento de A y U es U, la intersección deA y el complemento de U es el conjunto vacío, entonces A es igual o un subconjunto de U.
Esta conclusión forma parte de la definición de las partes de U, pero se puede llegar a ella por el cumplimiento de una de las cuatro condiciones expuestas, como ya se mencionó, las cuatro condiciones son equivalentes y el cumplimiento de una de ellas implica el cumplimiento de las demás.
Aplicando el mismo razonamiento podemos ver:

Siendo B un conjunto de las partes de U, llegando a la conclusión de que el conjunto vacío es igual o un subconjunto de B.







 , común en la tecnología digital, siendo la forma más usual y la más cómoda de representar.
, común en la tecnología digital, siendo la forma más usual y la más cómoda de representar.

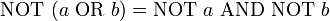

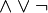 y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}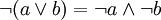

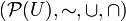
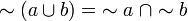
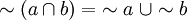


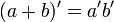


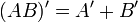

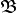 en este caso está formado por dos elementos {0,1}, o {F, V}, o {no, sí}, dos valores contrapuestos, que son las dos posibles alternativas entre dos situaciones posibles, aquí, sin perdida de la generalidad, tomaremos el conjunto: {0,1} como ya hemos dicho:
en este caso está formado por dos elementos {0,1}, o {F, V}, o {no, sí}, dos valores contrapuestos, que son las dos posibles alternativas entre dos situaciones posibles, aquí, sin perdida de la generalidad, tomaremos el conjunto: {0,1} como ya hemos dicho:



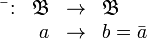






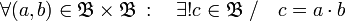


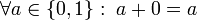



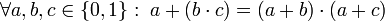


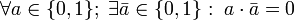

















 .
.
















 , para un U conocido, como álgebra de Boole si cumple las siguientes axiomas:
, para un U conocido, como álgebra de Boole si cumple las siguientes axiomas: